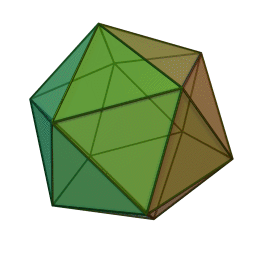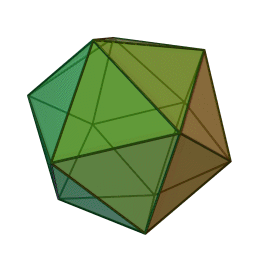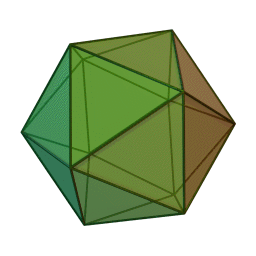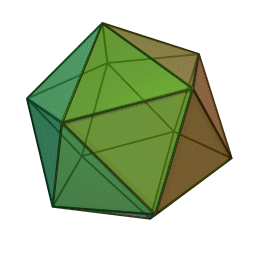
Caractéristiques de l’isocaèdre
- Un icosaèdre est un solide à trois dimensions faisant partie des polyèdres et comportant 20 faces.
- Le terme provient du grec « icos » signifiant « vingt ».
- Il existe divers types d’icosaèdres tels que l’icosaèdre régulier convexe, l’icosaèdre rhombique, le pseudo-icosaèdre, le grand icosaèdre et les solides de Johnson.
- Dans Timée, Platon a relié les cinq polyèdres réguliers convexes à des éléments de l’univers.
- Il a considéré l’icosaèdre comme représentatif de l’eau en raison de sa grande stabilité due à son nombre élevé de faces et de sommets par rapport aux autres quatre polyèdres.