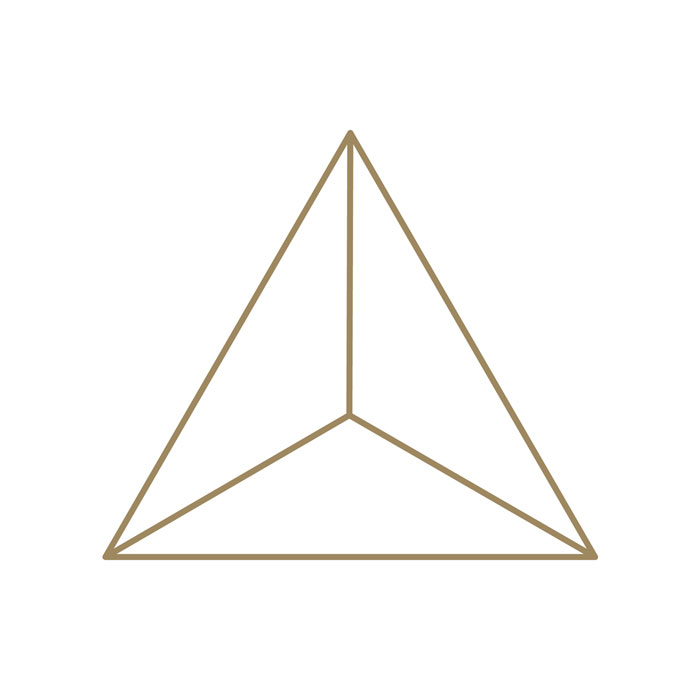
Caractéristiques du tétraèdre
- Un tétraèdre est un solide en forme de pyramide composé de quatre triangles.
- Il existe des tétraèdres réguliers, formés de quatre triangles équilatéraux. Ils font partie des cinq polyèdres réguliers ou solides de Platon.
- Il existe également des tétraèdres orthocentriques. Leurs quatre hauteurs qui se rejoignent en un point appelé l’orthocentre.
- Le volume d’un tétraèdre est égal à la base (qui est un triangle) multipliée par la hauteur (qui est la distance entre la base et le sommet) divisée par 3.
- Autrement dit, si on note B la base et h la hauteur, le volume V d’un tétraèdre est donné par la formule suivante : V = (B x h) / 3