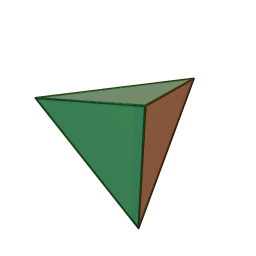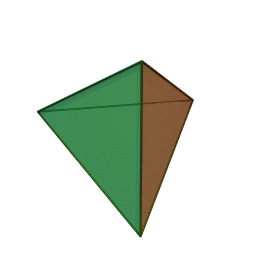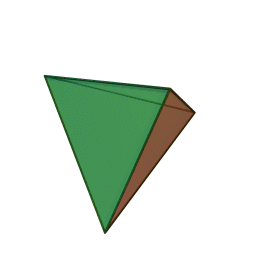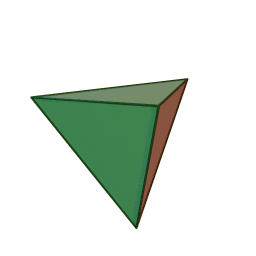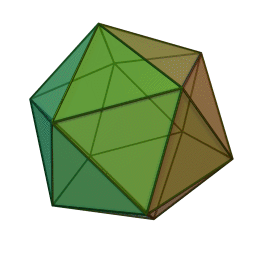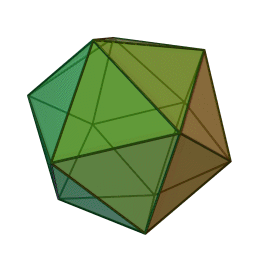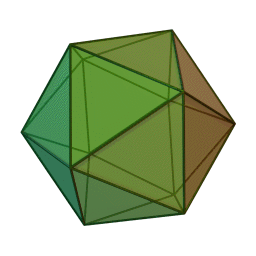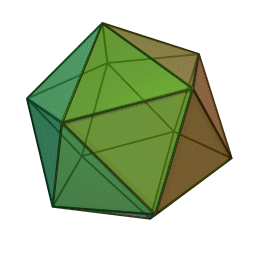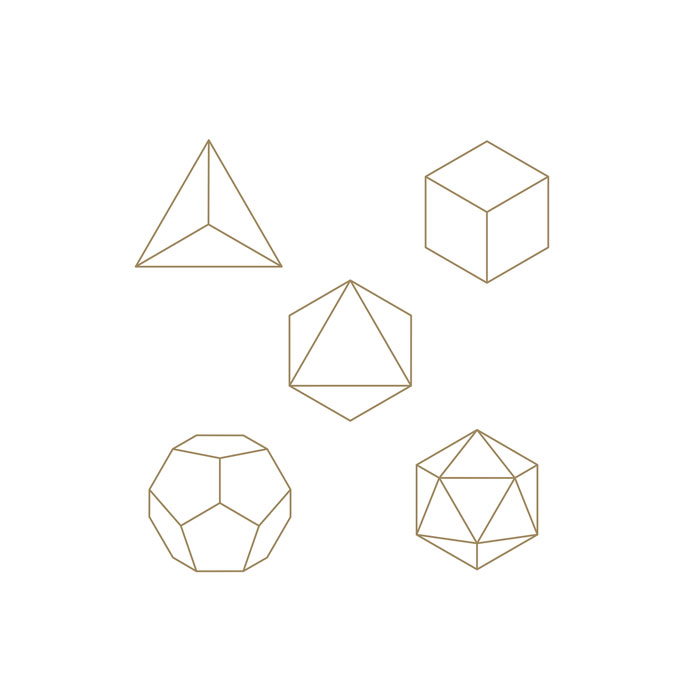
Caractéristiques des solides de Platon
- Les solides de Platon sont des formes géométriques régulières et convexes, qui se caractérisent par un nombre précis de faces.
- Il en existe cinq types, chacun désigné par son nombre de faces : le tétraèdre (4 faces), le hexaèdre ou cube (6 faces), l’octaèdre (8 faces), le dodécaèdre (12 faces) et l’icosaèdre (20 faces).
- Bien que leur nom fasse référence à Platon, ces solides ont été admirés pour leur esthétique et leurs symétries depuis l’antiquité.
- On associe quatre d’entre eux aux éléments de la physique antique, et le cinquième à la quintessence. Les solides de Platon font partie de la géométrie sacrée.