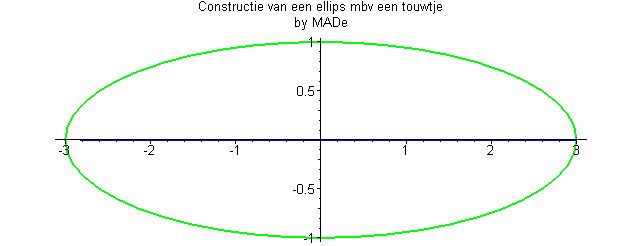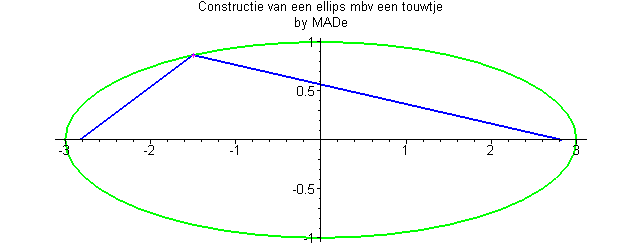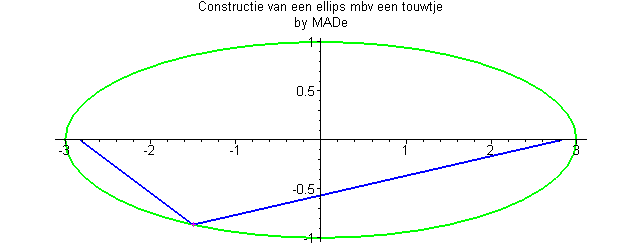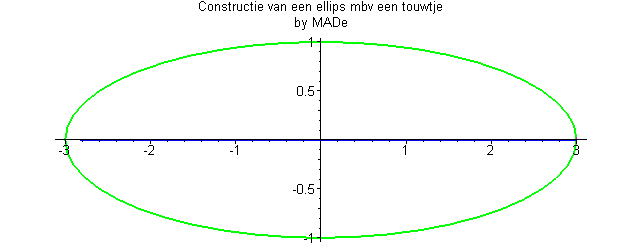
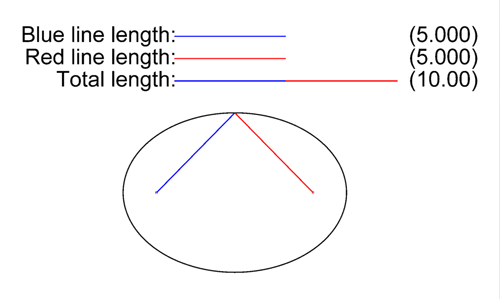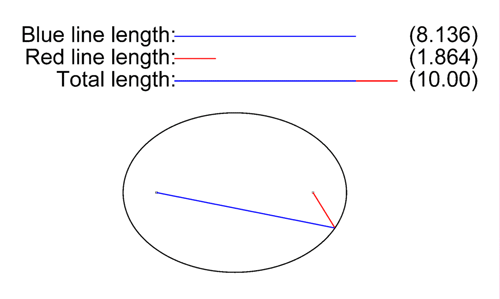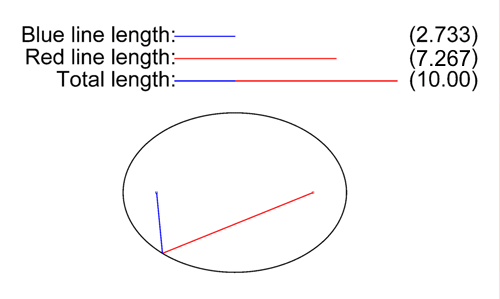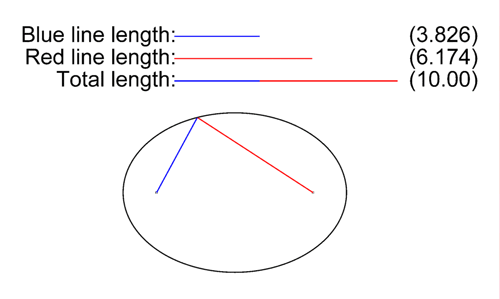
Caractéristiques de l’Ellipse
- L’ellipse est une courbe plane fermée qui résulte de l’intersection d’un cône ou cylindre avec un plan coupant l’axe de rotation.
- Elle appartient à la famille des coniques ayant une excentricité entre 0 et 1.
- Les points formant l’ellipse ont une somme de distances aux foyers constante.
- En vue de perspective, l’ellipse apparaît comme un cercle vu de biais ou l’ombre d’un disque sur une surface plane.
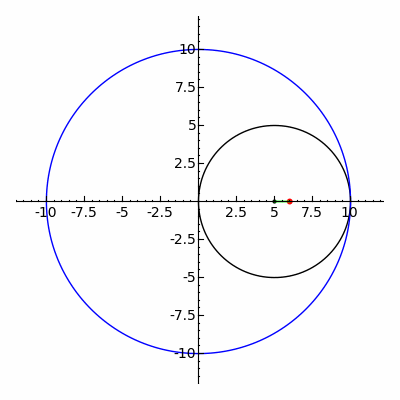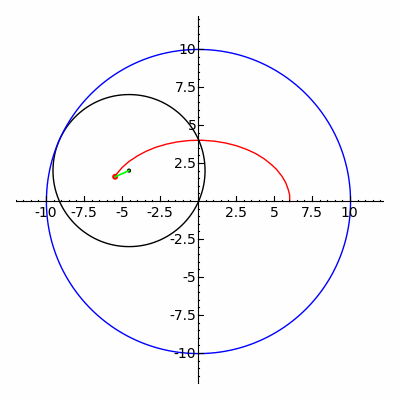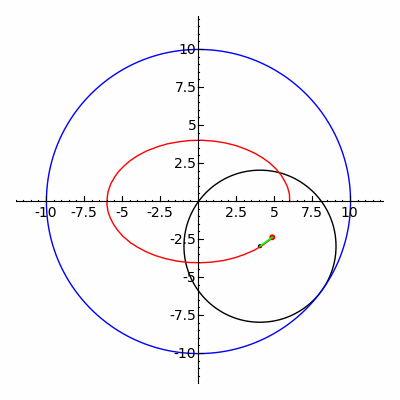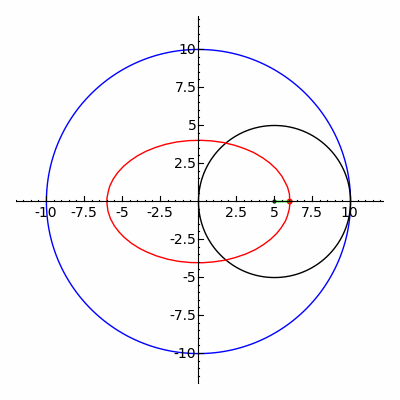
- En astronomie, les ellipses sont utilisées pour représenter les orbites des corps célestes, telles que l’orbite elliptique de la Terre autour du Soleil.